Metoda de coborâre infinită

L. Kurlyandchik, G. RosenblumMetoda a descendenței infinite
Care număr irațional este „cel mai vechi”? Fără îndoială, √ 2 . Nu știm exact cine a dovedit primul iraționalitatea acestui număr, dar suntem convinși că s-a făcut așa ceva.
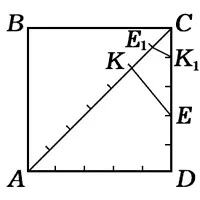
Deoarecec2 = 2a2, atunci
Astfel, triunghiulKEC, similar cu triunghiulACD, este isoscel dreptunghic și putem face aceeași construcție pe laturile sale ca și pe laturile triunghiuluiACD. Lăsați deoparte segmentulEK1 de [EC]:EK1 =KC; pe segmentul [KC]KE1:KE1 =K1C. PuncteleK1 șiE1 vor cădea din nou în punctele de divizare. TriunghiulK1CE1 va fi din nou isoscel dreptunghic. Pentru aceasta vom construi un triunghiK2CE2 în același mod; această procedură poate fi continuată pe termen nelimitat. În același timp, triunghiurileKjCEjdevin mai mici, dar de fiecare dată puncteleKjșiEjvor cădea în punctele inițiale de diviziune ale segmentelorACşiCD. Dar acesteadoar un număr finit de puncte! Și există infinit de multe triunghiuriKjCEj. Această contradicție demonstrează iraționalitatea lui √ 2 .
Au trecut secole. A apărut o demonstrație algebrică, poate mai simplă.
Iraționalitatea lui √ 2 înseamnă că ecuațiax2 = 2y2 nu are soluții în numere naturalex,y. Să presupunem că există astfel de soluții șix=m,y=neste una dintre ele.
Din ecuație rezultă cămeste un număr par,m= 2m1. Substituindm= 2m1 în ecuație, obținemn2 = 2m1 2 , adicăx=n,y=m1 este de asemenea o soluție. Rețineți căn2 = 2n1 2 . Astfel,x=m1,y=n1 soluție a ecuației, în timp cem1n>m1 >n1 > . și nu poate exista o succesiune infinită descrescătoare de numere naturale! Prin urmare, presupunerea noastră a fost greșită, iar numărul √ 2 este irațional.
Ambele argumente au urmat, în esență, același tipar: presupunând că problema are o soluție, am construit un fel de proces infinit, în timp ce, după însuși sensul problemei, acest proces trebuie să se termine undeva. O astfel de metodă se numeștemetoda coborârii infinite* .
Adesea metoda coborârii este aplicată într-o formă mai simplă. Presupunând că am ajuns deja la finalul natural al procesului, vedem că nu ne putem „opri”.
Fiex=m,y=nsoluție a ecuațieix2 = 2y2 cu cel mai micx. Numărulmtrebuie să fie par,m= 2m1, decix=m,y=m1 este, de asemenea, o soluție a ecuației noastre. Cu toate acestea,m>n, care contrazice alegerea soluțieim,nca „cea mai mică”.
Această versiune a dovezii arată că metoda coborârii este asemănătoare cu metoda inducției matematice. Ambele metode se bazează pe faptul că orice set nevid de numere naturale are un element minim. Metoda coborârii este cea mai convenabilă pentru demonstrarea teoremelor de „negare”.
Metoda de coborâre în probleme
Sarcina 1 .Demonstrați că ecuația este de nerezolvat în numere naturale
Soluție. Să presupunem că există soluții șix=m,y=n,z=p,t=rsoluție cu cel mai micxposibil. Din ecuație se poate observa căreste un număr par,r= 2r1.
Înlocuind această soluție în ecuație și împărțind la 2, obținem
Acum este clar căpeste par,p= 2p1, prin urmare,
Apoi procedăm în același mod:n= 2n1,
Deoarecex2 +y2 +z2 +t2 este un număr par, atunci printre numerelex,y,z,tun număr par de uni impar, adică fie patru, fie doi, fie zero. Dacă toate numerele sunt impare, atuncix2 +y2 +z2 +t2 este divizibil cu 4 și 2xyztnu este divizibil. Dacă există doar două numere impare, atuncix2 +y2 +z2 +t2 nu este divizibil cu 4, dar 2xyzteste împărțit. Prin urmare, toate numerele sunt pare, adicăx=x1,y=y1,z=z1,t=t1. Înlocuind aceste valori în ecuație, obținem
Ca și înainte, vedem că toate cele patru numere nu pot fi impare, altfelx1 2 +y1 2 +z1 2 +t1 2 nu este divizibil cu 8. Nici exact două numere nu pot fi impare, deoarece chiar și atuncix1 2 +y1 2 +z1 2 +t1 2 nu este divizibil cu 8. Deci, obținem că toate numerele sunt pare, adică
Argumentând ca înainte, obținem căx2,y2,z2,t2 numere pare și așa mai departe. Este ușor de înțeles că pentru oricesnaturale
Adică pentru orice număr naturals
numere întregi. Ei bine, acest lucru este imposibil pentru orice naturalx,y,z,t.
Și iată o ecuație care are infinit de soluții, dar care este investigată prin aceeași metodă.
Sarcina 3.Găsiți toate soluțiile în numere naturale ale ecuației
Soluție. Evident,x1 = 3,y1 = 2 este soluția acestei ecuații. Să demonstrăm că dacă perechea (x,y) este o soluție, atunci perechea (3x+ 4y, 2x+ 3y) este de asemenea o soluție. Aceasta rezultă din identitate
Am specificat o succesiune infinită de soluții (x1,y1), (x2,y2), . Să demonstrăm acum că nu există alte numere care să satisfacă ecuația.
Fie (x,y) să fie o soluție. În acest caz (3x4y, 3y2x) este de asemenea o soluție, deoarece
Din condiţia 9 = 9x2 18y2 > 2y2 implică faptul că 37x8 > 4y; iar pentruy> 2 din condiţia 4 = 4x2 8y2 2 rezultă că 3y> 2x. Adică, pentruy> 2 noi din soluție (x,y) obținem soluția (x(1) ,y(1) ) în mod natural numere, undex(1) (1) (n) ,y(n) ), undey(n) ≤ 2. Deoarecey(n) evident nu poate fi egal cu 1, atunciy(n) = 2. Prin urmare,x(n) = 3. Și aceasta înseamnă că numerelexșiyaparțin succesiunea construită anterior.
Până acum, am luat în considerare doar ecuații. Acum să rezolvăm problema „textului” cu metoda noastră.
Sarcina 4.Există2N+1greutăți, fiecare cântărind un număr întreg de grame.Se știe că oricare2Ndintre ele pot fi descompuse în scale, N pentru fiecare, în așa fel încât să ajungă la echilibru. Demonstrați că toate greutățile au aceeași greutate.
Soluție. Este clar că toate greutățile au simultan fie o pondere pară, fie o pondere impară: greutatea oricăror 2Ngreutăți este pară. Scădeți acum din greutățile tuturor greutăților greutatea celei mai ușoare greutăți (sau a celei mai ușoare, dacă sunt mai multe). Noul sistem de greutăți satisface evident și condiția problemei, iar printre greutăți se numără „greutăți” de greutate zero. Prin urmare, greutățile tuturor greutăților noului sistem sunt egale. Împărțind greutățile tuturor greutăților la jumătate, obținem din nou un sistem de greutăți care satisface condițiile problemei, printre care se numără „greutăți” de greutate zero. Prin urmare, din nou obținem că greutatea tuturor greutăților este egală și așa mai departe. Din „coborâre infinită” rezultă că toate „greutățile” sunt zero, iar aceasta înseamnă că toate greutățile inițiale au aceeași greutate.
Ideea de coborâre infinită ne permite să rezolvăm unele probleme de geometrie combinatorie.
Sarcina 5.Un cub poate fi tăiat în mai multe cuburi diferite?
Soluție. Să facem mai întâi o remarcă evidentă. Fie pătratulPsă fie împărțit într-un număr finit de pătrate diferite. Atunci cel mai mic pătrat nu este adiacent graniței pătratuluiP.
Să presupunem acum că cubulQa fost tăiat în diferite cuburiQj, fiePuna dintre fețeleQ. CuburileQjadiacentePgenerează o partițiePîn pătrate distincte în perechi. FieP1 cel mai mic dintre aceste pătrate,Q1 cubul corespunzător.P1 nu este adiacent granițeiP, prin urmare este înconjurat de pătrate mari. Cuburile corespunzătoare formează un „puț” care conține cubulQ1.
FieP'1 fața „superioară” (opusă fețeiP1) a cubuluiQ1. Cuba,adiacent laP'1 generează o partiție aP'1 în pătrate diferite. Din nou, cel mai mic dintre ele,P2, este situat în interiorulP'1, prin urmare, cuburile care înconjoară cubul corespunzătorQ2 sunt mai mari decâtQ2 şi formează din nou un „puţ”. Continuând construcția mai departe, vom obține un „turn” infinit format din cuburi în continuă scădere, iar acest lucru este imposibil.
În concluzie, o problemă pe hârtie în carouri.
Sarcina 6.Di o coală de hârtie în carouri. Demonstrați că pentrun≠ 4nu existăn-gon regulat cu vârfuri la nodurile rețelei.
Soluție. Mai întâi, demonstrăm că nu există un triunghi regulat cu vârfuri la noduri. Într-adevăr, fiealungimea laturii acestui triunghi; atuncia2 este un număr întreg după teorema lui Pitagora. Aria triunghiului estea2 √ 3 /4, adică este irațional. Pe de altă parte, este evident că aria oricărui poligon cu vârfuri la noduri este rațională.
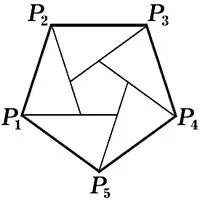
Fien≠ 3, 4, 6. Să presupunem căP1,P2, .Pnn-gon cu vârfuri la noduri. Deoparte de puncteleP1,P2, . VectoriPn8, respectiv egali cu vectoriiP827P83, 7P837P84, .P817P82 (vezi figura). Noile puncte vor cădea din nou în nodurile rețelei și vor forma unn-gon regulat în interiorul celui original. Cu nouln-gon, puteți face același lucru și așa mai departe, fără sfârșit. Cu toate acestea, pătratul lungimii laturiin-gonului este un număr întreg, iar în construcțiile noastre scade tot timpul!
Demonstrați că baza și latura unui triunghi isoscel cu un unghi de vârf de 36°incomensurabil.