Transformarea Fourier în acțiune identifică frecvența semnalului și evidențiază notele
Să începem cu pianul. Foarte simplificat, acest instrument muzical este un set de taste albe și negre, la apăsare, fiecare dintre ele produce un anumit sunet de o frecvență prestabilită de la joasă la înaltă. Desigur, fiecare instrument cu claviatura are propriul timbru unic de sunet, datorită căruia putem distinge, de exemplu, un acordeon de un pian, dar, în linii mari, fiecare tastă este doar un generator de unde acustice sinusoidale de o anumită frecvență.
Atunci când un muzician cântă o compoziție, el apăsă și eliberează alternativ sau simultan tastele, drept urmare mai multe semnale sinusoidale se suprapun unul altuia formând un model. Este acest desen pe care îl percepem ca pe o melodie, datorită căruia putem recunoaște cu ușurință o lucrare interpretată pe diverse instrumente în diferite genuri sau chiar fredonată neprofesionist de o persoană.
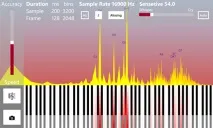
Ilustrarea vizuală a notației muzicale
Detectarea frecvenței (mod tuner pentru chitară)

Sarcina inversă este de a dezasambla compoziția muzicală care sună în note. Adică, descompuneți semnalul acustic total captat de ureche în sinusoidele originale. De fapt, acest proces este o transformată Fourier directă. Iar apăsarea tastelor și extragerea sunetului este procesul transformării Fourier inverse.
Matematic, în primul caz, o funcție periodică complexă (pe un anumit interval de timp) este extinsă într-o serie de funcții ortogonale mai elementare (sinus și cosinus). Și în al doilea, însumarea lor inversă, adică sinteza unui semnal complex.
Ortogonalitatea, în unelegen, denotă nemiscibilitatea funcțiilor. De exemplu, dacă luăm câteva bucăți de plastilină colorată și le lipim împreună, atunci putem în continuare să vedem ce culori au fost inițial, dar dacă amestecăm bine mai multe borcane de vopsele pentru guașă, atunci va fi imposibil să restabilim cu precizie culorile originale. fara informatii suplimentare.
(!) Este important să înțelegematunci când ne angajăm să analizăm un semnal real folosind transformata Fourier, idealizăm situația și pornim de la presupunerea că acesta este periodic în intervalul de timp curent și este format din sinusoide elementare. Adesea, acesta este exact cazul, deoarece semnalele acustice, de regulă, sunt de natură armonică, dar sunt în general posibile cazuri mai complexe. Oricare dintre ipotezele noastre despre natura semnalului duce de obicei la distorsiuni și erori parțiale, dar fără aceasta este extrem de dificil să extragem informații utile din acesta.
Acum descriem întregul proces de analiză mai detaliat:
1. Totul începe cu faptul că undele sonore vibrează membrana unui microfon, ceea ce le transformă în oscilații analogice ale unui curent electric.
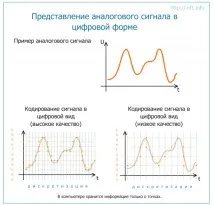
2. Apoi există oeșantionarea semnalului electric analogic în formă digitală. În acest moment, merită să ne gândim în detaliu.
Deoarece semnalul analogic constă matematic dintr-un set infinit de valori de puncte-amplitudine continue în timp, în timpul procesului de măsurare putem extrage din acesta doar o serie finită de valori în puncte discrete de timp, adică, de fapt, efectuează cuantificarea timpului...
De regulă, citirile sunt luate la intervale de timp egale mici, adică cu o anumită frecvență, de exemplu, 16000 sau 22000 Hz. Cu toate acestea, în cazul general, citirile discrete pot merge și inegale, dar acest lucru complică aparatul matematicanaliză, deci nu este folosită de obicei în practică.
Există o importantăteoremă a lui Kotelnikov-Nyquist-Shanon, care afirmă că un semnal periodic analogic cu un spectru finit (limitat în lățime) poate fi restaurat în mod unic fără distorsiuni și pierderi în eșantioanele luate cu o frecvență mai mare. mai mult sau egal cu de două ori frecvența superioară a spectrului (numită frecvență de eșantionare sau Nyquist).
Pentru această recuperare este necesar să se aplice funcții speciale de interpolare, dar problema este că atunci când se folosesc aceste funcții, calculele trebuie efectuate pe un interval de timp infinit, ceea ce este imposibil în practică. Prin urmare, în viața reală, este imposibil să creșteți artificial rata de eșantionare fără distorsiuni, chiar dacă inițial satisface teorema Kotelnikov-Nyquist-Shanon. Pentru această operație se folosesc filtre Farrow.
De asemenea, discretizarea are loc nu numai în timp, ci și în ceea ce privește nivelul valorilor de amplitudine, deoarece computerul este capabil să manipuleze doar un set limitat de numere. De asemenea, introduce mici erori.
3. În etapa următoare, are loc în sinetransformata Fourier directă discretă.
Selectăm un cadru scurt (interval) al compoziției, constând din eșantioane discrete, pe care în mod convențional le considerăm periodice și îi aplicăm transformata Fourier. Ca rezultat al transformării, obținem o serie de numere complexe care conțin informații despre spectrele de amplitudine și fază ale cadrului analizat. Mai mult, spectrele sunt, de asemenea, discrete cu un pas egal cu (frecvența de eșantionare) / (număr de eșantioane). Adică, cu cât luăm mai multe mostre, cu atât obținem o rezoluție mai precisă a frecvenței. Cu toate acestea, la o rată de eșantionare constantă, prin creșterea numărului de probe, noimărim intervalul de timp analizat, iar din moment ce în lucrările muzicale reale notele au durate sonore diferite și se pot înlocui rapid între ele, ele sunt suprapuse, astfel încât amplitudinea notelor lungi „umbrește” amplitudinea celor scurte. Pe de altă parte, pentru tunerele de chitară, acest mod de creștere a rezoluției frecvenței funcționează bine, deoarece nota, de regulă, sună lung și una.
Există, de asemenea, un truc destul de simplu pentru a crește rezoluția frecvenței - trebuie să umpleți semnalul discret original cu zerouri între eșantioane. Cu toate acestea, ca urmare a unei astfel de umpleri, spectrul de fază este puternic distorsionat, dar rezoluția de amplitudine crește. De asemenea, este posibil să utilizați filtre Farrow și să creșteți artificial frecvența de eșantionare, cu toate acestea, acest lucru introduce și distorsiuni în spectre.
Durata cadrului este de obicei între aproximativ 30 ms și 1 s. Cu cât este mai scurtă, cu atât obținem o rezoluție mai bună în timp, dar mai proastă ca frecvență, cu cât eșantionul este mai lung, cu atât mai bună ca frecvență, dar mai proastă în timp. Acest lucru amintește foarte mult deprincipiul de incertitudine al lui Heisenbergdin mecanica cuantică..și nu este ușor, așa cum spune Wikipedia,relația de incertitudine din mecanica cuantică în sens matematic este o consecință directă a proprietăților transformata Fourier...
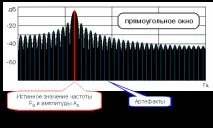
De asemenea, este interesant faptul că, ca urmare a analizei unei mostre dintr-un singur semnal sinusoidal, spectrul de amplitudine este foarte similar cu un model de difracție ...
Un semnal sinusoidal limitat de o fereastră dreptunghiulară și „difracția” acesteia
Difracția undelor luminoase

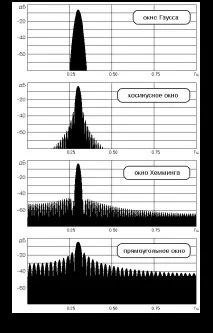
În practică, acesta este un efect nedorit care face dificilă analiza semnalelor, așa că încearcă să-l reducă folosind funcții de fereastră. Există o mulțime de astfel de funcții, mai jos sunt implementărileunele dintre ele, precum și efectul comparativ asupra spectrului unui singur semnal sinusoidal.
Aplicarea unei funcții de fereastră la un cadru de intrare este foarte simplă:
În ceea ce privește computerele, algoritmulFast Fourier Transforma fost dezvoltat în timp util, ceea ce minimizează numărul de operații matematice necesare pentru a-l calcula. Singura cerință a algoritmului este ca numărul de eșantioane să fie un multiplu al unei puteri de doi (256, 512, 1024 și așa mai departe).
Mai jos este implementarea sa clasică recursivă în C#.
Există două variante ale algoritmului FFT, decimat în timp și decimat în frecvență, dar ambele produc rezultate identice. Funcțiile preiau o serie de numere complexe umplute cu valori reale ale amplitudinilor semnalului în domeniul timpului, iar după executarea lor returnează o serie de numere complexe care conțin informații despre spectrele de amplitudine și fază.Merită să ne amintim că părțile reale și imaginare ale unui număr complex sunt departe de a fi aceleași cu amplitudinea și faza acestuia!
magnitudine = Math.Sqrt(x.Real*x.Real + x.Imaginar*x.Imaginar) faza = Math.Atan2(x.Imaginar, x.Real)
Matricea rezultată de numere complexe este exact pe jumătate plină cu informații utile, cealaltă jumătate este doar o imagine în oglindă a primei și poate fi ușor exclusă din considerare. Dacă vă gândiți bine, acest moment ilustrează bine teorema Kotelnikov-Nyquist-Shanon, că frecvența de eșantionare ar trebui să fie nu mai mică decât frecvența maximă dublată a semnalului ...
Există, de asemenea, o variație a algoritmului FFT fără recursiunea Cooley-Tukey, care este adesea folosită în practică, dar este puțin mai dificil de înțeles.
Imediat după calcularea transformării Fourier, este convenabil să normalizați amplitudineagamă:
Acest lucru va duce la faptul că mărimea valorilor de amplitudine va fi de același ordin, indiferent de dimensiunea eșantionului.
După ce s-au calculat spectrele de amplitudine și frecvență, este ușor să procesați semnalul, de exemplu, aplicați filtrarea frecvenței sau efectuați compresia. De fapt, așa puteți face un egalizator: prin efectuarea unei transformări Fourier directe, este ușor să creșteți sau să micșorați amplitudinea unui anumit interval de frecvență și apoi să efectuați o transformată Fourier inversă (deși egalizatoarele reale se bazează de obicei pe o principiu diferit - defazarea semnalului). Da, iar comprimarea semnalului este foarte simplă - trebuie doar să faci un dicționar, unde cheia este frecvența, iar valoarea este numărul complex corespunzător. În dicționar, trebuie să introduceți doar acele frecvențe, amplitudinea semnalului la care depășește un anumit prag minim. Informațiile despre frecvențele „liniștite” care nu sunt audibile de ureche se vor pierde, dar se va obține o compresie vizibilă, menținând în același timp o calitate acceptabilă a sunetului. În parte, acest principiu stă la baza multor codecuri.
4. Detectare precisă a frecvenței
Transformarea Fourier discretă ne oferă un spectru discret, în care fiecare valoare a amplitudinii este separată de vecinii săi prin intervale egale de frecvență. Și dacă frecvența în semnal este un multiplu al unui pas egal cu (frecvența de eșantionare) / (numărul de eșantioane), atunci vom obține un vârf ascuțit pronunțat, dar dacă frecvența semnalului se află undeva între treptele adiacente mai aproape de mijloc, vom obține un vârf cu vârf „tăiat” și ne va fi greu de spus care este frecvența. Se poate foarte bine ca semnalul să conţină două frecvenţe situate una lângă alta. Aceasta este limitarea rezoluției în frecvență. La fel ca într-o fotografie cu rezoluție scăzută, obiectele mici se lipesc împreună și devin imposibil de distins, la fel și detaliile fine.spectrul poate fi pierdut.
Dar frecvențele notelor muzicale se află cu mult dincolo de grila pașilor de transformare Fourier, iar pentru sarcinile de zi cu zi de acordare a instrumentelor muzicale și de recunoaștere a notelor, este necesar să se cunoască exact frecvența exactă. Mai mult, la octave joase cu o rezoluție de 1024 de eșantioane și mai jos, grila de frecvență Fourier devine atât de rară încât mai multe note încep pur și simplu să se potrivească într-un singur pas și devine practic imposibil să se determine care dintre ele cântă de fapt.
Pentru a ocoli cumva această limitare, uneori sunt folosite funcții de aproximare, de exemplu, cele parabolice. www.ingelec.uns.edu.ar/pds2803/Materiales/Articulos/AnalisisFrecuencial/04205098.pdf mgasior.web.cern.ch/mgasior/pap/biw2004_poster.pdf Dar acestea sunt toate artificiale măsuri , care, îmbunătățind unii indicatori, pot da distorsiuni în alții.
Există o modalitate mai naturală de a determina cu precizie frecvența?Da, și este ascunsă tocmai în utilizarea spectrului de fază al semnalului, care este adesea neglijat. Această metodă de rafinare a frecvenței semnalului se bazează pe calcularea întârzierii de fază a spectrelor a două cadre suprapuse unul peste altul, dar ușor deplasate în timp.
În C#, implementarea metodei pare destul de simplă:
Aplicarea este, de asemenea, ușoară:
De obicei, cadrele sursă sunt deplasate cu 1/16 sau 1/32 din lungimea lor, deci ShiftsPerFrame este 16 sau 32.
Ca urmare, vom obține un dicționar frecvență-amplitudine, unde valorile frecvenței vor fi destul de apropiate de cele reale. Totuși, „vârfurile tăiate” vor fi în continuare observate, deși mai puțin pronunțate. Pentru a elimina acest dezavantaj, puteți pur și simplu să le „terminați”.
Analiza notelor operelor muzicale deschide o serie de posibilități interesante. La urma urmei, având un desen muzical gata făcut, poțicaută alte compoziții muzicale cu un model similar.
De exemplu, aceeași lucrare poate fi interpretată pe un instrument diferit, într-un mod diferit, cu un timbru diferit, sau transpusă în octave, dar modelul muzical va rămâne similar, ceea ce vă va permite să găsiți versiuni diferite ale aceleiași lucrări. Este foarte asemănător cu jocul „ghici melodia”.
În unele cazuri, o astfel de analiză va ajuta la identificarea plagiatului în lucrările muzicale. De asemenea, conform desenului muzical, teoretic, puteți căuta lucrări de o anumită dispoziție sau gen, ceea ce ridică căutarea la un nou nivel.
Acest articol subliniază principiile de bază ale determinării cu acuratețe a frecvențelor semnalelor acustice și ale izolării notelor. De asemenea, arată o conexiune intuitivă subtilă a transformării Fourier discrete cu fizica cuantică, ceea ce încurajează gândirea la o imagine unificată a lumii.