Sensul mecanic al derivatei a doua

Fie ca punctul material să se miște rectiliniu conform legii s=s(t), unde s este calea parcursă de punctul în timp t. Atunci viteza v a acestei mișcări este v= s'(t) = v(t), adică. este, de asemenea, o funcție a timpului.

La momentul t, viteza are valoarea v=v(t). Să luăm în considerare un alt moment de timp t+Δt. Ea corespunde valorii vitezei v1 = v(t+Δt). Prin urmare, incrementul de timp Δt corespunde incrementului de viteză Δv= v1 – v = v(t + Δt) – v(t). Atitudine

se numește accelerația medie pe intervalul de timp Δt.

Accelerația la un moment dat t este limita accelerației medii la Δt→0:

Astfel, accelerația mișcării rectilinie a unui punct este derivata vitezei în raport cu timpul. Dar după cum am văzut deja, viteza este derivata traseului s în raport cu timpul t: v = s'. Având în vedere acest lucru, avem:

acestea. accelerația mișcării rectilinie a unui punct este egală cu derivata a 2-a a drumului în raport cu timpul

43. Diferențiale. Sensul geometric al diferenţialului. proprietăți diferențiale.

Diferenţiale

Pentru funcții

Diferenţialul unei funcţii într-un punct poate fi definit ca o funcţie liniară

unde denota derivata in punctul .

Astfel, există o funcție a două argumente.

Diferenţialul poate fi definit direct, adică fără a implica definirea derivatei, ca o funcţie care depinde liniar de şi pentru care următoarea relaţie este adevărată

Pentru afișaje

Diferenţialul unei mapări într-un punct este un operator liniar astfel încât condiţia

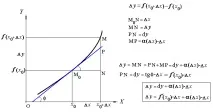
Semnificația geometrică a diferenţialului

Diferenţiala funcţiei f(x) în punctul x0 este egală cu incrementul pe care o primeşte ordonata tangentei la curba y=f(x) cu abscisa în punctul x0 la trecerea de la punctul de contact în punctul cu abscisa x0+Δx.

Proprietăți diferențiale

Diferenţialul unei funcţii are proprietăţi similare cu cele ale unei derivate.

1.Diferenţiala constantei este egală cu zero: dc = 0, с = const.

2.Diferenţiala sumei funcţiilor diferenţiabile este egală cu suma diferenţialelor termenilor:

Consecinţă. Dacă două funcții diferențiabile diferă printr-un termen constant, atunci diferențialele lor sunt

d(u+c) = du (c= const).

3.Diferenţialul produsului a două funcţii diferenţiabile este egal cu produsul primei funcţii cu diferenţa celei de-a doua plus produsul celei de-a doua cu diferenţa primei:

Consecinţă. Factorul constant poate fi scos din semnul diferenţialului

d(cu) = cdu (c = const).

4.Diferenţialul u/v a două funcţii diferenţiabile u = u(x) şi v = v(x) este definită prin formula

5. Proprietatea de independenţă a formei diferenţialului faţă de alegerea unei variabile independente (invarianţa formei diferenţialului): diferenţialul unei funcţii este egal cu produsul derivatei şi diferenţialul argumentului, indiferent dacă acest argument este o variabilă independentă sau o funcţie a unei alte variabile independente.

44. Teoreme de bază ale calculului diferenţial (teorema lui Fermat, teorema lui Rolle, teorema lui Lagrange).

Teorema lui Fermat

Teorema afirmă că:

Pentru orice număr natural, ecuația nu are soluții naturale și .

Teorema lui Rolle

(Teorema lui Rolle ) Fie funcțiaf(x)

1. continuă pe segmentul [a,b];
2. diferențiabil în interval (a,b);
3. la capetele segmentului [a,b] ia valori egale.

Apoi există un punctcO (a,b) astfel încâtf'(c) = 0.

Dovadaeste dată în I.M. Petrushko și L.A. Kuznetsova „Curs de matematică superioară: Introducere în analiza matematică. calcul diferențial.” M.: Editura MEI, 2000. Pg. 118.

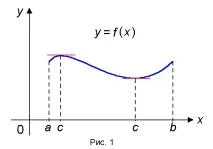
Interpretarea geometrică a teoremei lui Rolle

Din teorema lui Rolle rezultă că există un punct cu O (a,b) în care tangenta la graficul funcțieif(x) este paralelă cu axa OX(Fig. 1).

Teorema lui Lagrange

(Teorema lui Lagrange ) Fie funcțiaf(x)

Apoi există un punct cu O (a,b) astfel încât

f(b) -f(a) =f'(c) (b−a) .

(1)

Formula (1) se numeșteFormulă Lagrange sauFormulă de increment finit

Dovadaeste dată în I.M. Petrushko și L.A. Kuznetsova „Curs de matematică superioară: Introducere în analiza matematică. calcul diferențial.” M.: Editura MEI, 2000. Pg. 119.

---