CUNOAȘTE INTUIT, Prelegere, Colorare grafice
Conjectura în patru culori
De mai bine de o sută de ani, matematicienii au încercat să demonstreze conjectura în patru culori. S-au înregistrat progrese semnificative în această direcție. În presă a apărut un mesaj (K.Appel, W.Haken, Every planar map is four colorable, Bull. of Amer. Math . Soc., 82, \No\,5 (sept. 1976)), că ipoteza de patru culori a fost fundamentată cu ajutorul unui computer.
Să formulăm, fără dovezi, câteva rezultate legate de această problemă.
- Dacă ipoteza în patru culori nu este adevărată, atunci orice exemplu care o infirmă va fi foarte dificil. Se știe, de exemplu, că fiecare graf planar având mai puține vârfuri este 4-colorabil.
- Orice graf planar care nu conține triunghiuri este 3-colorabil (teorema lui Gretch).
- Dacă încercăm să demonstrăm conjectura în patru culori, atunci este suficient să o demonstrăm pentru graficele planare hamiltoniene (un rezultat destul de neașteptat al lui Whitney).
Carti de colorat
Apariția ipotezei celor patru culori este asociată istoric cu colorarea hărților geografice. Dacă există o hartă care arată mai multe țări, atunci este interesant de știut de câte culori sunt necesare pentru a colora aceste țări în așa fel încât să nu fie pictate două țări vecine în aceeași culoare. Poate cea mai familiară formă a ipotezei cu patru culori este că orice hartă poate fi colorată cu patru culori.
Pentru a face această afirmație corectă, trebuie să definim ce înseamnă cuvântul „hartă”. Deoarece problemele de colorare pe care le luăm în considerare impun ca țările situate pe ambele părți ale marginii să fie de culori diferite, va trebui să excludem hărțile care au un pod. Astfel, este convenabil să definiți o hartă ca un graf planar conex care nu conține punți. Rețineți că, cu această definiție a hărții,excludeți buclele sau marginile multiple.
Numim o hartă colorabilă dacă fețele sale pot fi colorate cu vopsele, astfel încât două fețe adiacente, adică fețe ale căror limite au o margine comună, să nu fie de aceeași culoare. Acolo unde este posibil să fim confuzi, vom folosi termenul de colorabilitate la vârf, adică colorabilitate în sensul descris mai sus. De exemplu, graficul de mai jos este 3-colorabil și 4-vertex-colorable.
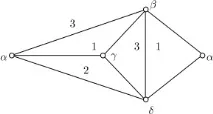
Acum formulăm conjectura în patru culori pentru hărți: fiecare hartă este de 4 culori.
Teorema 8.3. O hartă este 2-colorabilă dacă și numai dacă este un grafic Euler.
DovadaOrice vârf de la trebuie să fie înconjurat de un număr par de fețe, deoarece acestea pot fi colorate în două culori. Rezultă că gradul fiecărui vârf este par și, prin urmare, este un graf Euler.
Curba Jordan, sau arcul Jordan, pe un plan se numește curbă continuă care nu are auto-intersecții; O curbă închisă Jordan este o curbă Jordan al cărei început și sfârșit coincid.
Să descriem o metodă care oferă colorarea dorită a fețelor graficului. Selectați o față arbitrară și colorați-o în roșu. Să desenăm o curbă Jordan dintr-un punct al feței până la un punct al oricărei fețe și în așa fel încât această curbă să nu treacă prin niciun vârf al graficului. Dacă pe drumul de la un punct la un punct al unei fețe curba noastră traversează un număr par de muchii, colorăm fața în roșu; altfel, albastru.
Este ușor să arătăm că colorarea este bine definită: luăm un „ciclu” format din două astfel de curbe Jordan (adică o curbă Jordan închisă) și arătăm că intersectează un număr par de muchii ale graficului (trebuie să folosim inducția pe numărul de vârfuri din interiorul ciclului și Astafaptul că fiecare vârf al graficului are un număr par de muchii incidente).